How does Temperature changes the behaviour of the LLM's response?
How does the temperature parameter changes the distribution probability of the next token?
Ever played around with the response of an LLM and seen someone complaining that it's not consistent—so, as a fix, you reduce the temperature parameter while calling the LLM via an SDK?
Ever wonder what exactly happens with the temperature parameter, why exactly reducing the temperature parameter makes the LLM’s response more consistent, and increasing the temperature makes it more inconsistent?
In this particular article, I’m going to cover this specific area of an LLM’s response and how exactly the probability distribution changes when this parameter is adjusted, along with the math behind it. I’ll also add a small example to help us understand the concept better.
I am assuming here, you know how a transformer architecture works, more importantly, what all steps are between an input text and the final probability distribution.
Table of contents
Quick recap: Transformer Architecture and the Final Layer of the Transformer
How does the temperature parameter play a role in changing this distribution?
Quick recap: Transformer Architecture and the Final Layer of the Transformer
So before we deep dive, I just want to quickly cover how processing happens in a Transformer, and a bit about the final layer—also called the output layer—of the Transformer.
What exactly happens in the background when we ask a particular question into ChatGPT?
At a very high-level overview, this is the usual process:
Text input broken down into tokens
Each token has a pre-defined embedding associated with it.
The entire set of tokens is then post-processed with layers of Self-Attention and Feed-Forward Neural Network.
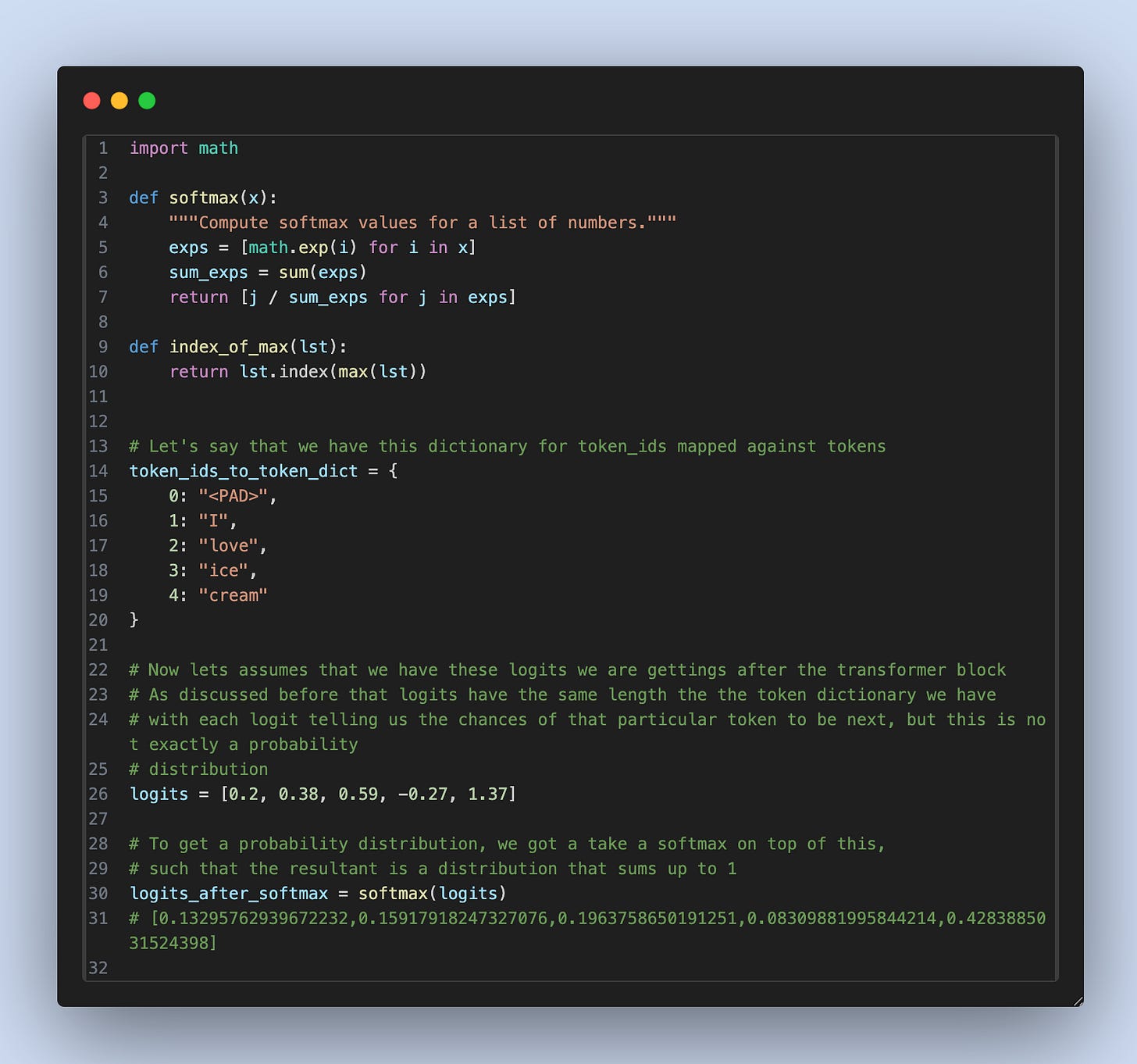
At the end of this Transformer block, we get logits. One key thing to note here is that the logits are of size
vocab_size—In other words, they indirectly represent the probability distribution of all possible next tokens for the given set of input tokens.
How we reach this probability distribution is the story of another article. But we are assuming that we have the particular logits, which are the next token prediction probability distribution.
Let’s look at some code to understand how we infer what the next token is once we have the logits ourselves.
As you can see, the 4th token has the highest probability of .42% which indirectly means that if we do sampling 100 times, 42 times, the next token the transformer will predict will be the 4th token, cream in our case.
Now, if we use simple reasoning—if we can change this probability distribution to favor one particular token much more than the others—then we can definitely control the behavior of LLMs, and vice versa. That’s where the temperature comes into the picture.
How does the temperature parameter play a role in changing this distribution?
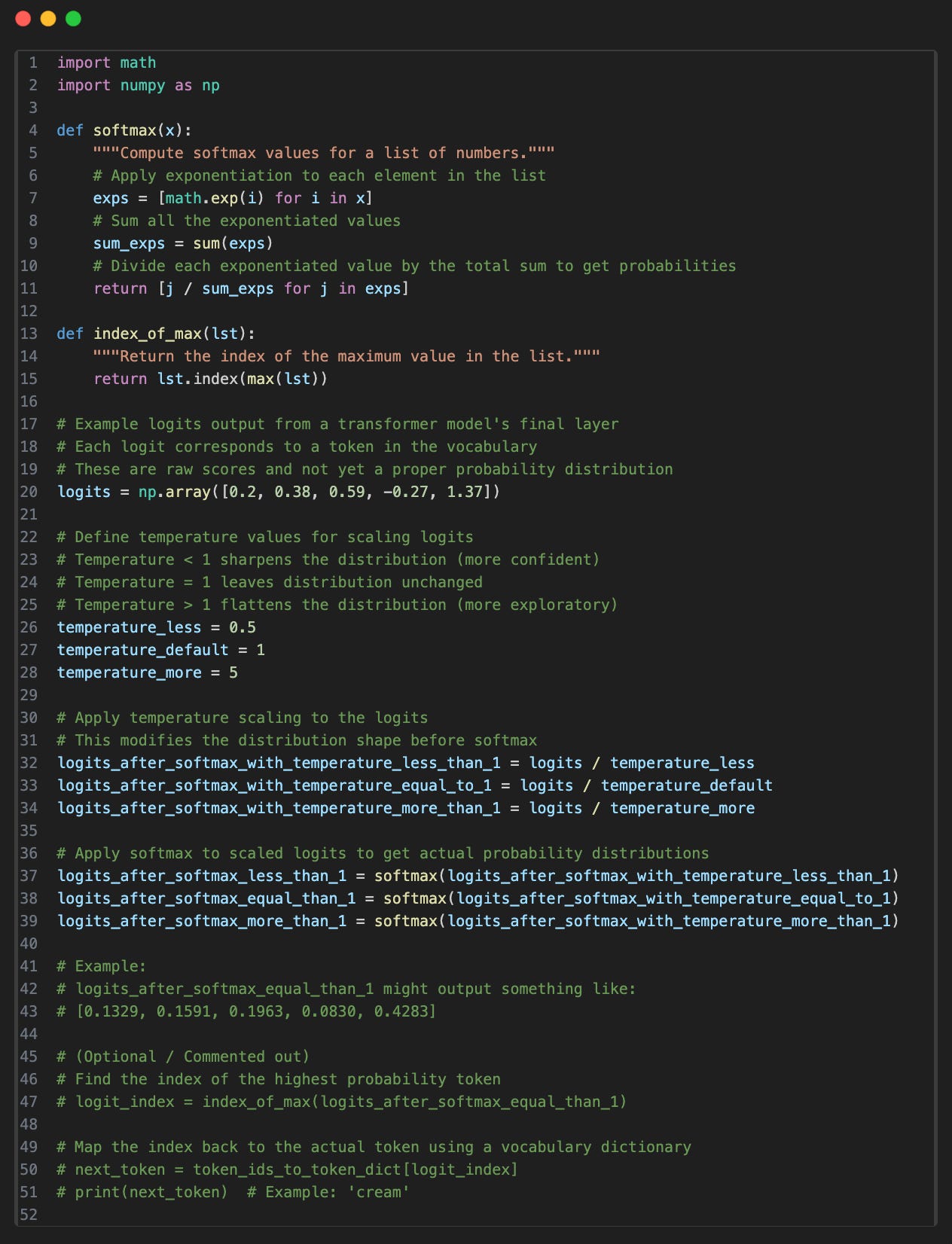
Now, a simple way to change this probability distribution, which we get after the transformer block, is by scaling it with a factor; this factor is what we call temperature.
The logits we get after the transformer block are divided by the temperature parameter and then fed to the softmax function to make the final probability distribution.
Let’s understand theoretically what happens when we use different temperature value?
Temperature = 1: This is the default value. It doesn’t really affect the probability distribution—what we get is simply what the Transformer has predicted.
Temperature < 1: In this case, each value in the logits increases relative to its magnitude—the higher the value, the more it increases. After applying softmax, the probability distribution becomes sharper, with clearer peaks, leading to more consistent next-token predictions.
Temperature > 1: When the temperature is greater than 1, the probability distribution flattens out. This means the model sees more equal chances among the next tokens, resulting in more mixed or varied behavior while predicting the next token.
Let’s now see this with an example code.
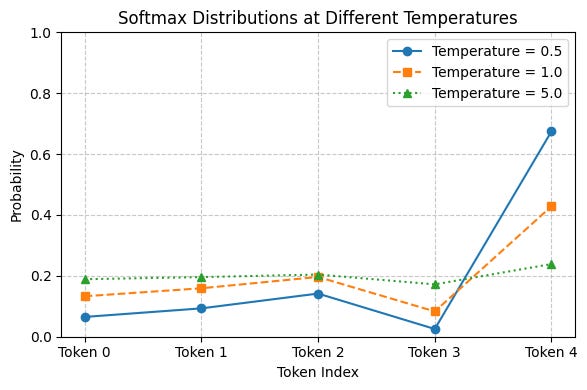
This is the final softmax probability distribution
As you can see, the more the temperature value, the flatter the probability distribution is, and therefore, lesser consistency in the nature of LLM’s response.
Here is the link to the GitHub Repository, which contains all this code: Link